内容

ソート

クイックソート

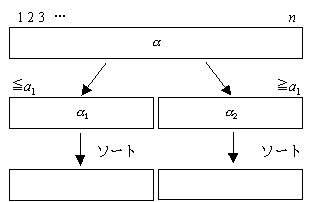
クイックソートはn個のデータの系列(a₁, a₂,…, a_n)を先頭の数値a₁を基準にして次のように2つの系列α₁、α₂に分割する。

α₁ : a₁と同じかa₁より小さな数値からなる系列。

α₂ : a₁と同じかa₁より大きな数値からなる系列。

このように分割し、a₁とa₂をそれぞれソートして得られた2つの系列を接続すればソートされる。特に、 a₁とa₂を配列の中に順に置いてソートすれば系列の接続は必要ない。a₁とa₂のソーティングはいまと同じ処理を繰り返せば良いのでマージソートと同じく関数の再帰呼び出しで実現できる。

分割の処理は以下のように実現できる。

この処理は配列a[s..e]に入っている系列を基準を基にして2つに分割する。基準と同じか基準より小さい数値がa[s..q]に移され、基準と同じか基準より大きい数値がa[p..e](p = q + 1)に移される(pとqが逆のことに注意)。p = q + 2となる場合があるが、このときはa[s..q]、a[q+1](=基準)、a[p..e]の3つに分割される。

クイックソートの場合、基準点の選び方が計算スピードを左右する。そのため、分割の基準となる値の決め方を、例えば系列中のいくつかの数値の中央値とするように工夫する場合がある。

各アルゴリズムの計算量

選択法、挿入法、バブルソート、マージソート、クイックソートそれぞれの計算量は以下のとおりである。

ソートする数をnとすると選択法の計算量はO(n²)となる。選択法では、入力が既にソート済みであってもO(n²)回の比較が行われる。

それに対し、挿入法、バブルソートは既にソート済みの系列にはO(n)ですむ。しかし、どちらのアルゴリズムも逆順にソートされている場合にはO(n²)となり、任意に並んでいる場合でも、平均の計算量はO(n²)となる。

マージソートとクイックソートは、対象となる問題をいくつかの部分問題に分割し、それらを解いて得られた解を統合してもとの問題の解を得るという分割統治法に基づいたアルゴリズムである。

マージソートの計算量はO(n log n)となり、上の3つのアルゴリズムに比べると格段の高速化が図られている。また、クイックソートも最悪の場合O(n²)となるが、入力の系列が一様な並びの場合、平均計算量はO(n log n)となる。

このように、同じソートを行う処理でも、アルゴリズムによって実行スピードには大きな差が生まれる。